Hebel-Rolle-Pyramide
Hier geht es darum, herauszufinden, wie die Ägypter - ohne Strom und Benzin - die Pyramiden gebaut haben.
Bei dieser Gelegenheit können wir das Mathewissen der 3. und 4. Klasse anwenden. Wir müssen multiplizieren und dividieren.
Wie groß ist die Cheops-Pyramide?
Um sich das besser vorstellen zu können, vergleichen wir sie mit der Höhe unserer Kirche. Da wir nur ein Bild von der Kirche haben, müssen wir den Maßstab der Pyramide auf den der Kirche umrechnen.
Noch beeindruckender ist der Vergleich mit unserem Dorf. Wir stellen die Cheops-Pyramide in das Satellitenbild unseres Dorfs. Nun heißt es, die Kantenlänge der Pyramide auf den Maßstab unseres Bildes umzurechnen.
Bilddatei "" in der Kategorie "" nicht vorhanden
Jetzt wird uns die beeindruckende Größe klar:
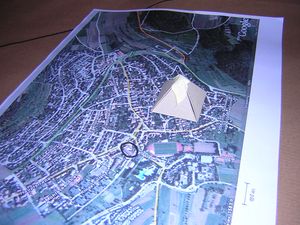

Wie kann man ohne Bagger und Kräne ein solches Bauwerk errichten?
Wahrscheinlich hatten die Ägypter noch keine Räder und Achsen. Außerdem wären die vermutlich aus Holz gebaut und hätten dem tonnenschweren Gewicht der Steine nachgegeben.Es funktioniert viel besser mit Baumstämmen als Rollen.
Wir probieren das mit einem Mauerstein aus, den wir auf Rundhölzern voranschieben. Dabei wird hinten immer wieder ein Holz frei, dass wir wieder nach vorne legen. So können wir beliebige Distanzen überbrücken - allerdings mit jeder Menge Baumstamm-Schleppen...

Wie überwinden wir die Höhe ohne Kran
Die schiefe Ebene macht uns das Leben leichter. Wir können nun unseren Stein viel leichter nach oben rollen, müssen dafür aber eine größere Strecke zurücklegen.
Kleine Kraft - Großer Weg
Der Hebel wandelt - genauso wie die schiefe Ebene - eine große Kraft in eine viel kleinere. Dafür muss man einen größeren Weg zurücklegen.Wir rechnen das aus und wenden es gleich an der Wasserflasche an, die wir mit einen Hebel anheben.

Es wird wie immer gebastelt - Die Rechenwaage
Unsere Waage setzt das Hebelgesetz ein, um einfache Rechenaufgaben zu lösen.Legt man die Cent-Stücke auf die unterschiedlichen Markierungen der Hebelarme, so kann man einfache Gleichungen experimentell lösen:
Zum Beispiel:
Hebellänge 2 x 2 Münzen = Hebellänge 4 x 1 Münze.
Also 2 x 2 = 4
Oder komplizierter
Hebellänge 1 x 3 Münzen + 3 x 2 Münzen = Hebellänge 9 x 1 Münze.
Also 1 x 3 + 3 x 2 = 9
